Tutorial
Neuronale Netze - 0. allgemeine Grundlagen
Neuronale Netze - 0. allgemeine Gundlagen
0.1. Einleitung
Zum besseren Verständnis soll in diesem Abschnitt auf die wesentlichen Grundlagen der neuronalen Netze eingegangen werden. Dabei werden besonders Aktivierungsfunktionen und einige Lernarten etwas detailierter betrachtet.
0.2. Aufbau eines Verarbeitungselementes - künstliches Neuron
Das künstliche Neuron hat sein Vorbild in der Natur und stellt somit dessen, mit den Möglichkeiten der Technik realisierten, "Bruder" dar. Zum Überblick soll folgende Grafik dienen.
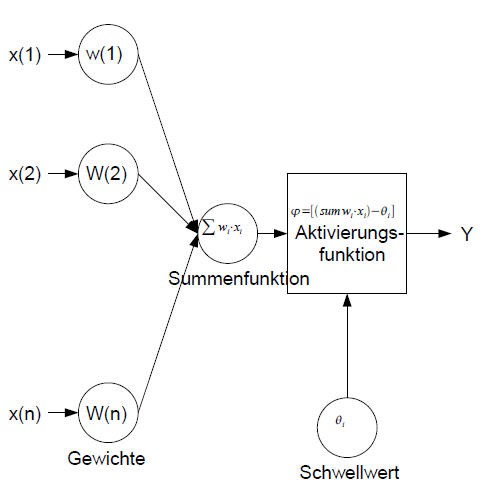
Die Werte x(1)..x(0) bilden die Eingangswerte, diese können diskret bzw. kontinuierlich sein, jedem Eingangswert ist eine Gewichtung zugeordnet. Demnach besitzt ein Neuron die gleiche Anzahl von Gewichtungen und Eingangswerten. Es folgt eine Summenfunktion, die jeden einzelnen Eingangswert mit dessen Gewichtung multipliziert und anschließend alle Werte miteinander addiert.
Mit dem Summenwert des gesamten Netzwerkes wird die Aktivierungs-Funktion bedient, welche den Ausgang des Neurons bestimmt.
0.3. Summenfunktion
Wie das Modell des künstlichen Neurons zeigt, besteht ein wesentlicher Teil des Neurons aus der Summenfunktion. Dahinter versteckt sich, wie es der Name schon sagt, eine Summierung der Eingangswerte * Gewichtungen. Man könnte auch sagen das künstliche Neuron stellt einen kontinuierlichen Summierer dar, welcher alle Eingangswerte (abhängig von Gewichten) addiert und weiterleitet. Die Art, wie das summierte Signal zu interpretieren ist, ist abhängig von der Aktivierungsfunktion. Vereinfacht stellt sich der Sachverhalt so dar, die Summenfunktion ist die Sekretärin, welche das Wesentliche sammelt und gebündelt dem Chef, der Aktivierungsfunktion, zur Entscheidung übergibt.
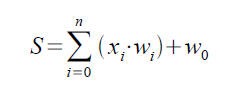
0.4. Aktivierungsfunktionen
Wie bereits erwähnt, stellt die Aktivierungsfunktion den Ausgang des Netzwerkes zur Verfügung. Im einfachsten Fall beträgt der Ausgang des Neurons entweder Null oder Eins. Diese Art von Funktionen nennt man Schwellenwertfunktion :
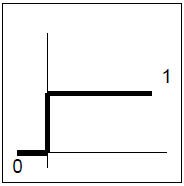
Keine Angst vor Formeln, es besagt der Ausgang entweder Null oder Eins ist. Man stelle sich eine Toilettenspühlung vor, beim unterschreiten des minimalen Wasserstanden, also nach dem Spühlen, wird das Wasserventil schlagartig geöffnet und das Wasserreservat füllt sich, beim Überschreiten des vorgegebenen Wasserstandes wird der Wasserzulauf schlagartig geschlossen. Natürlich ist es in unserem Fall genau umgekehrt, liefert die Summenfunktion einen Wert größer gleich Null, so wird der Ausgang schlagartig Eins, ansonsten ist er Null. Rein formal wird diese Funktion wie folgt beschrieben :
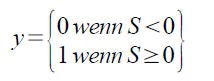
Eine weitere Art ist die Aktivierung mit Hilfe einer stückweise Linearen Funktion :
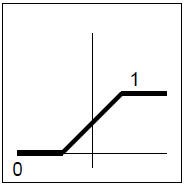
Zum besseren Verständnis kann sich jeder seine Stereoanlage vorstellen, der Regler für laut und leise ist oftmals ein einfaches Potentiometer (regelbarer Wiederstand). Der Wiederstand als Funktion des Stromes und der Spannung ist, genau wie ein Teil unserer Aktivierungsfunktion, linear. Die Obergrenze in unserem Steroanlagen - Beispiel sei die maximale Lautstärke und die Untergrenze die minimale Lautstärke, also Null - alles, was dazwischen ist wird linear geregelt, wobei Strom und Spannung gleichmäßig größer bzw. kleiner werden. Die Mathematik hat oftmals einen Hang zur Dramatik und beschreibt diesen Sachverhalt so :
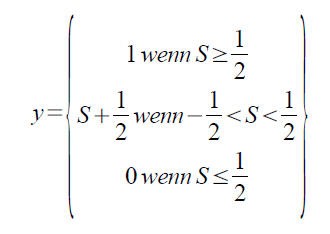
Die letzte Art der Aktivierungsfunktionen ist eine Schwanenhalsfunktion, auch Sigmoide Funktion genannt. Wer jetzt an die WC-Ente denkt, liest sich wahrscheinlich das falsche Tutorial durch ... (kleiner Scherz am Rande). Der Name Schwanenhalsfunktion ist als Synonym für das folgende Schaubild zu verstehen :
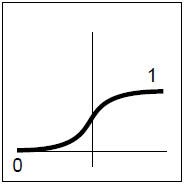
Ein passendes Beispiel für diese Funktion zu finden, ist nicht einfach - besser, mir ist keins eingefallen. Wie man der Grafik entnehmen kann, ist die Funktion nicht gerade, also nicht linear, sondern eine Kurve, die im unendlich kleinen als auch im unendlich großen gegen die zwei Grenzwerte, in unserem Fall 0 und 1, strebt. Gerade diese "Nichtgeradheit" ermöglicht es den betreffenden Verarbeitungselementen Problemstellungen zu bewältigen, die mit einem rein linearen Ausgang unmöglich sind (siehe XOR Problem und das Perceptron). Die Formel lautet :
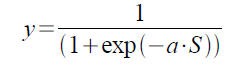
0.5. Lernen
Nachdem wir das künstliche Neuron etwas durchleuchtet haben, möchte ich auf einen entscheidenden Absatz eingehen - das Lernen. Ich möchte auf die Frage, was Lernen wirklich ist, nicht zu sehr eingehen, da sich eine rein philosophische Debatte über dieses Thema nicht vermeiden lässt. Für unseren Fall reicht es, wenn wir sagen, dass das Lernen für neuronale Netze nichts anderes bedeutet, als die Gewichtungen in der Art zu verändern, dass beim Anlegen eines Eingangsmusters ein gewünschter Ausgang produziert wird.
In diesem Zusammenhang muss auf den Begriffe der "Synaptische Plastizität" (Änderung der Stärke der synaptischen, in unserem Fall gewichtsabhängigen, Übertragung) eingegangen werden, wobei besonders ein gewisser Herr "Donald Olding Hebb" erwähnt werden muss. Dieser formulierte, zwar nicht als erster, die nach ihm benannte Lernregel (Hebbsche Lernregel). Welche nichts anderes bedeutet, als dass zwei Verarbeitungselemente sich bei öfterer gegenseitiger Aktivierung aufeinander einspielen. Dabei werden die Verbindungen zwischen diesen beiden Verarbeitungselementen gestärkt. Diese Verstärkung wird als "Potenzierung" und eine Abschwächung der Verbindung als "Depression" bezeichnet. Die Abschwächung bzw. Verstärkung der einzelnen Neuronenverbindungen, welche im Folgenden durch Gewichtungen repräsentiert werden, stellen das eigentliche Gedächtnis dar, der Weg zum trainierten Gedächtnis wird als Lernprozess bezeichnet.
Anhang
Formelbezeichnungen :
- S - Summenfunktion; S = x(n)*w(n)+x(n-1)*w(n-1)+ ... + x(1)*w(1) + w(0)
- a - Steigungsmaß
| Zusätzliche Informationen und Funktionen |
|---|
- Das Tutorial wurde am 28.12.2007 von
 chutullu angelegt. chutullu angelegt.
- Die aktuellste Version wurde am 22.01.2008 von
 chutullu gespeichert. chutullu gespeichert.
|
|
 chutullu
chutullu
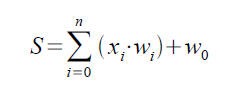

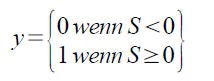

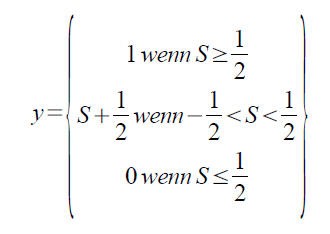

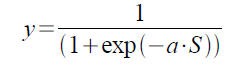



 FreeBASIC-Nachrichten jetzt auch über Twitter erhalten. Follow us!
FreeBASIC-Nachrichten jetzt auch über Twitter erhalten. Follow us! Bearbeiten
Bearbeiten Versionen
Versionen