Code-Beispiel

Polynomiale Ausgleichskurve (X-Regression)

Lizenz:	Erster Autor:	Letzte Bearbeitung:
k. A.	TJF	07.11.2011

Polynomregression 4. Grades

Dieses Beispiel betrifft ein mathematisches Verfahren der Regressionsanalyse (auch Anpassung, Parameterschätzung, Ausgleichsrechnung oder Fitting genannt). Einzelheiten können diesem Wikipedia-Artikel entnommen werden.

Messwerte Yi, welche an diskreten Stellen Xi vorliegen, werden durch eine Funktion y = F(x) abgebildet, wobei die Funktion F(x) durch ein Polynom beliebigen Grades gebildet wird. Der vorliegende Beispiel-Code berechnet die Parameter Ai des Polynoms

F(x) = A0

     + A1 x

     + A2 x^2

     + A3 x^3

     + ...

     + An x^n

so, dass die Abweichung zwischen dem Polynom und den Stützstellen minimal wird.

Mit Hilfe der Polynomialen Ausgleichskurve können dann Werte zwischen den vorliegenden Stützstellen interpoliert werden oder der Verlauf der Meßkurve kann extrapoliert werden. Auch wird es möglich, die Ableitung einer Meßkurve mit Hilfe der bekannten Polynomparameter zu berechnen.

Das Beispiel besteht aus zwei Teilen:

der Definition einer allgemeinen TYPE-Struktur (UDT) und
einem Anwendungsbeispiel derselben.

1) TYPE-Struktur

Die TYPE-Struktur enthält die mathematische Berechnung der Polynom-Parameter mit Hilfe von Verfahren der Linearen Algebra, weshalb die Bibliothek libFBla (benötigt und) eingebunden wird. Der folgende Code sollte unter dem Namen "PolReg.bas" abgespeichert werden:

' This is file "PolReg.bas"

' (C) LGPLv2 by Thomas[ dot ]Freiherr{ at }gmx{ dot }net



#INCLUDE ONCE "libFBla.bas"



TYPE Polynom

  AS LA_S StDev

  AS LA_V PolPara

  DECLARE CONSTRUCTOR(BYVAL Order AS UINTEGER, BYVAL M AS LA_M PTR, _

                      BYVAL ChX AS UINTEGER = 0, BYVAL ChY AS UINTEGER = 1)

  DECLARE PROPERTY Val_(BYVAL X AS LA_S) AS LA_S

END TYPE



' computes a polynom for data in matrix V

' ChX = column of X positions (default = 0)

' ChX = column of measurement values (default = 1)

' berechnet ein Polynom vom Grad Order aus den Werten in Matrix V

' ChX = Spalte der X-Positionen (Default = 0)

' ChY = Spalte der Meßwerte (Default = 1)

CONSTRUCTOR Polynom(BYVAL Order AS UINTEGER, BYVAL V AS LA_M PTR, _

                    BYVAL ChX AS UINTEGER = 0, BYVAL ChY AS UINTEGER = 1)

  VAR az = V->Row_()

  IF az < Order THEN ?"Error: not enough values" : EXIT CONSTRUCTOR

  ' prepare variables for the gradient equations

  ' coefficient matrix m and solution vector n

  ' Variablen fuer Berechnung der Normalengleichungen

  VAR m = LA_M(Order + 1), n = LA_V(Order + 1)



  ' compute matrix (one triangle) and vector elements

  ' berechnen: Dreiecksmatrix und Lösungsvektor

  FOR k AS INTEGER = 0 TO az

    FOR i AS INTEGER = 0 TO Order

      FOR j AS INTEGER = 0 TO i

        m.Set_(j, i, m.Val_(j, i) + V->Val_(k, ChX) ^ (i + j))

      NEXT

      n.Val_(i) = n.Val_(i) + V->Val_(k, ChY) * V->Val_(k, ChX) ^ i

    NEXT

  NEXT

  ' mirror triangle matrix / Dreiecksmatrix spiegeln

  FOR i AS INTEGER = 1 TO Order

    FOR j AS INTEGER = 0 TO i - 1

      m.Set_(i, j, m.Val_(j, i))

    NEXT

  NEXT



  ' compute the polynom parameters / Polynom-Parameter berechnen

  PolPara = n / m



  ' compute the standard deviation / Standardabweichung berechnen

  FOR i AS INTEGER = 0 TO az

    StDev += (Val_(V->Val_(i, ChX)) - V->Val_(i, ChY)) ^ 2

  NEXT

END CONSTRUCTOR



' comupte the value of the polynom at position X

' Berechnet den Wert des Polynoms an Position X

PROPERTY Polynom.Val_(BYVAL X AS LA_S) AS LA_S

  WITH PolPara

    VAR r = .Val_(0)

    FOR i AS INTEGER = 1 TO .Ubound_()

      r += .Val_(i) * X ^ i

    NEXT : RETURN r

  END WITH

END PROPERTY

Anwendung

Die Berechnung der Polynom-Parameter erfolgt im CONSTRUCTOR des UDTs. Dieser wird bei der Dimensionierung aufgerufen ( VAR Pol = Polynom(Order, @m) ).
Der Polynomgrad wird durch den Parameter Order bestimmt.
Die Wertepaare (Position Xi, Meßwert Yi) werden in der Matrix m (2 dimensionales Feld vom Typ LA_M) übergeben. Standardmäßig werden die X-Werte aus der Spalte 0 und die Y-Werte aus der Spalte 1 gelesen.
Alternative Spaltennummern können bei Bedarf in den Parametern ChX (= Channel X) und ChY definiert werden, z. B. falls die Matrix mehrere Meßkurven enthält.
Der Funktionswert des Polynoms an der Stelle x wird durch Pol.Val_(x) berechnet.
Die Polynomparameter können aus Pol.PolPara.Val_(n) gelesen werden (0 <= n <= Order). PolPara ist vom Typ LA_V und kann entsprechend verwendet/ausgegeben werden.
Die Standardabweichung des Polynoms wird im CONSTRUCTOR berechnet und kann aus Pol.StDev gelesen werden.

2) Anwendungsbeispiel

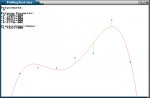
Die Stützstellen dieses Beispiels sind einem Diagram des o. g. Wikipedia-Artikels entnommen.

' This is file "PolReg_test.bas"

' (C) GPLv3 by Thomas[ dot ]Freiherr{ at }gmx{ dot }net



' Find more info at

'   http://en.wikipedia.org/wiki/Linear_least_squares_(mathematics)

' Weitere Informationen siehe

'   http://de.wikipedia.org/wiki/Methode_der_kleinsten_Quadrate



#INCLUDE ONCE "vbcompat.bi"



' specify output format / Ausgabeformat spezifizieren

#DEFINE LA_FORMAT(_V_) FORMAT(_V_, "+#.0000e+000")

#DEFINE LA_TR !"\n"



' Try also SINGLE precision / Versuche SINGLE Berechnung

'TYPE AS SINGLE LA_S

'#DEFINE LA_Eps (1e-6)



#INCLUDE ONCE "PolReg.bas"





'#DEFINE english



' print out headers and values / Ausgabe Ueberschrift und Werte

#MACRO HEADER(_G_, _E_, _T_)

 #IFDEF english

   ?:?_E_

 #ELSE

   ?:?_G_

 #ENDIF

 ?_T_

#ENDMACRO





' *** main ***

' here is the data input / Positionen X und Messwerte Y

VAR m = LA_M("1, 2" NL _

             "2, 2.5" NL _

             "3, 2.5" NL _

             "4, 3.4" NL _

             "5, 3.75" NL _

             "6, 6.7" NL _

             "7, 3")



' prepare output window / Ausgabefenster vorbereiten

CONST ScW = 639, ScH = 399

SCREENRES ScW + 1, ScH + 1, 8

WINDOWTITLE "PolRegTest.bas"

COLOR 0, 15

VAR Xm = 8, st = 2 * Xm / ScW

WINDOW (0, 0) - (Xm, 8)



VAR Order = 0 ' start order (simple average) / Start mit Mittelwert

DO

  CLS

  VAR Pol = Polynom(Order, @m)



  HEADER("Polynomgrad:", _

         "Polynomial order:"     , Order)

  HEADER("Polynom-Parameter:", _

         "Polynomial parameters:", Pol.PolPara)

  HEADER("Standardabweichung:", _

         "Standard deviation:"   , LA_FORMAT(Pol.StDev))

  HEADER("Taste druecken!", _

         "Press a key!", "")



  ' draw polynom / zeichne Polynomiale Ausgleichsfunktion

  PSET (0, Pol.Val_(0)), 4

  FOR x AS LA_S = st TO Xm STEP st

    LINE - (x, Pol.Val_(x)), 12

  NEXT



  ' draw measurement points / zeichne Messpunkte und Residuen

  FOR i AS INTEGER = 0 TO m.Row_()

    VAR x = m.Val_(i, 0), y = m.Val_(i, 1)

    LINE (x, y) - (x, Pol.Val_(x)), 10 '                    Residuen

    CIRCLE (x, y), st, 9, , , , F '                       Messpunkte

  NEXT



  ' wait for key press to compute next step / warten auf Tastendruck

  SLEEP

  SELECT CASE INKEY

  CASE CHR(27) : EXIT DO

  CASE CHR(255, 75), CHR(255, 80)

    Order -= 1 : IF Order < 0 THEN Order = m.Row_()

  CASE ELSE

    Order += 1 : IF Order > m.Row_() THEN Order = 0

  END SELECT

LOOP UNTIL INKEY = CHR(27)

Anmerkungen:

Der Grad des Polynoms darf die Anzahl der Stützstellen nicht überschreiten (, sonst wird das Gleichungssystem singulär = unlösbar).
Bei großem Polynomgrad können numerische Probleme auftreten (, durch Addition sehr kleiner und sehr großer Werte, sowie durch große Zahlen außerhalb des Wertebereiches des verwendeten Variablentyps LA_S). Ggf. ist es sinnvoll, die Stützstellen in das Intervall [-1, 1] zu transformieren, bzw. bei sehr vielen Stützstellen auch die Erstellung der Normalen-Gleichungen (im CONSTRUCTOR) in mehreren Einzelsummen zu erwägen.
Die Regression ist immer von einer einzigen Variablen x abhängig. Für zweidimensionale Regression (x, y) müssen die Ansatzfunktionen orthogonal sein, vgl. X/Y-Regressionsanalyse.

English

See english forum.

Zusätzliche Informationen und Funktionen

Das Code-Beispiel wurde am 07.11.2011 von TJF angelegt.
Die aktuellste Version wurde am 07.11.2011 von TJF gespeichert.

Bearbeiten

Versionen