Code-Beispiel

Fast Fourier Transformation (FFT)

Lizenz:	Erster Autor:	Letzte Bearbeitung:
LGPL	TJF	26.10.2014

Dieses Beispiel betrifft die Fast Fourier Transformation, eine häufig in der Regelungstechnik angewandte Umwandlung eines Signals vom Zeitbereich in den Frequenzbereich. Und natürlich kennen wird Frequenzspektren aus EDV Programmen (Audio-Applikationen) oder von der Stereoanlage.

Im Beispiel wird zunächst eine Klasse für komplexe Zahlen definiert. Mit ein wenig Vektorrechnung läßt sich dann die folgende Klasse für die FFT übersichtlicher gestalten.

In der Klasse FftUDT wird Speicher für zwei Felder reserviert, einerseits für Winkelwerte (W) und andererseits ein Feld für temporäre Zwischenwerte. Daher muss dem CONSTRUCTOR die Anzahl der Werte (Stützstellen) bekannt gegeben werden, die später berechnet werden sollen.

Die eigentliche Berechnung erfolgt dann in der Funktion Fft(). Das Zeitsignal wird als Feld von Vektoren an die Funktion übergeben. Die Berechnung erfolgt rekursiv. Beim Start muss der zweite Parameter Az gleich sein mit dem Wert, der dem CONSTRUCTOR übergeben wurde. Die Dimensionierung eines zusätzlichen Vektorfeldes für das Ergebnis (vgl. fbmath) ist nicht notwendig, das Eingabe-Vektorfeld wird mit dem Berechnungsergebnis überschrieben.

CONST PI = 4 * ATN(1)



TYPE AS DOUBLE float



TYPE Vektor

  AS float R, I

  DECLARE PROPERTY length AS float

END TYPE



PROPERTY Vektor.length AS float

  RETURN SQR(R * R + I * I)

END PROPERTY



OPERATOR + (BYREF X AS Vektor, BYREF Y AS Vektor) AS Vektor

  RETURN TYPE<Vektor>(X.R + Y.R, X.I + Y.I)

END OPERATOR



OPERATOR - (BYREF X AS Vektor, BYREF Y AS Vektor) AS Vektor

  RETURN TYPE<Vektor>(X.R - Y.R, X.I - Y.I)

END OPERATOR



OPERATOR * (BYREF X AS Vektor, BYREF Y AS Vektor) AS Vektor

  RETURN TYPE<Vektor>(X.R * Y.R - X.I * Y.I, X.R * Y.I + X.I * Y.R)

END OPERATOR





TYPE FftUDT

  AS ULONG Az

  AS Vektor PTR T, W

  DECLARE CONSTRUCTOR(BYVAL AS ULONG)

  DECLARE DESTRUCTOR()

  DECLARE SUB Fft(BYVAL AS Vektor PTR, BYVAL AS ULONG, BYVAL AS LONG)

END TYPE



CONSTRUCTOR FftUDT(BYVAL N AS ULONG)

  Az = N

  W = ALLOCATE(SIZEOF(Vektor) * Az * 2) '          ankles (Winkel) field

  T = W + Az '                                            temporary copy



  VAR d = 2 * PI / Az

  FOR i AS LONG = 0 TO Az - 1 '       generate sinus / cosinus tables

    VAR a = d * i

    W[i].R = COS(a)

    W[i].I = SIN(a)

  NEXT

END CONSTRUCTOR



DESTRUCTOR FftUDT()

  IF W THEN DEALLOCATE(W) : W = 0

END DESTRUCTOR



SUB FftUDT.Fft(BYVAL Q AS Vektor PTR, BYVAL N AS ULONG, BYVAL K AS LONG)

  IF N = 2 THEN

    VAR i = K + 1 _

      , b = Q[K] _

      , a = Q[I]



    Q[K] = b + a

    Q[I] = b - a

    EXIT SUB

  ENDIF



  VAR ndiv2 = N SHR 1

  FOR i AS LONG = 0 TO ndiv2 - 1

    VAR        a = K + 2 * i

            T[i] = Q[a]

    T[i + ndiv2] = Q[a + 1]

  NEXT



  FOR I AS LONG = 0 TO N - 1

    Q[k + i] = T[i]

  NEXT



  Fft(Q, ndiv2, K)

  Fft(Q, ndiv2, K + ndiv2)



  VAR j = Az \ N

  FOR i AS LONG = 0 TO ndiv2 - 1

    VAR x = W[i * j] * Q[K + ndiv2 + i] _

      , a = K + i



            T[i] = Q[a] + x

    T[i + ndiv2] = Q[a] - x

  NEXT



  FOR I AS LONG = 0 TO N - 1

    Q[K + i] = T[i]

  NEXT

END SUB







'' ***** main *****

'                 !!! Az <= SCREENWIDTH * 2, SY4 <= SCREENHEIGHT \ 4 !!!

CONST Az = 1 SHL 11, SX = Az SHR 1, SY4 = 140 '           some constants

VAR test = NEW FftUDT(Az) '                                    the class



DIM AS vektor values(Az -1) '                                 some input

VAR k = 2

FOR i AS LONG = 0 TO az - 1

  VAR d = 2 * pi * i / az

  values(i).r = 80 * (SIN(d * 32) + .25 * SIN(d * k)) '  sinus and noise

  k += 9

  IF k > az \ 2 THEN k = 2

NEXT



SCREENRES SX, 4 * SY4, 32 '                                 draw a curve

LINE (0, SY4 + values(0).R)-(0, SY4 + values(1).R)

FOR I AS LONG = 2 TO Az - 1

  LINE - (I \ 2, SY4 + values(I).R)

NEXT



SLEEP

test->Fft(@values(0), Az, 0) '                                    do FFT



DIM AS float res(Az \ 2 - 1) '                         the result vector



VAR Mx = values(0).length

FOR i AS LONG = 1 TO Az \ 2 - 1 '     search maximum, compute scaling

  res(i) = values(i).length

  Mx = IIF(res(i) > Mx, res(i), Mx)

NEXT : IF Mx THEN Mx = SY4 * 2 / Mx ELSE Mx = 0



VAR sym = SY4 * 4

FOR I AS LONG = 0 TO Az \ 2 - 1 '         draw the frequency spectrum

  LINE (I, sym)-(I, sym - res(I) * Mx)

NEXT



SLEEP

DELETE test

English

See english forum thread.

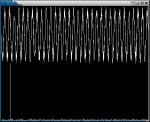
Zeitsignal (oben) und Frequenzspektrum

Zusätzliche Informationen und Funktionen

Das Code-Beispiel wurde am 07.01.2014 von TJF angelegt.
Die aktuellste Version wurde am 26.10.2014 von TJF gespeichert.

Bearbeiten

Versionen