• Tutorials
• Downloads
• Referenz
• NoPaste
• FAQ

Tutorial

Winkelmodus und Winkelfunktionen

von ytwinky

Seite 1 von 2

Winkelmodus
Was ist das denn? Nun, es ist einfach die Art und Weise, in der Winkel berechnet werden, vergleichbar mit Meilen und Kilometern.
Grundlage für die Winkel ist der Einheitskreis(Kreis mit dem Radius 1). Der Kreisumfang, also die Zahl seiner Einzelteile errechnet sich, wie bei einem Kreis üblich, per 2*Pi*r und da r=1 ist, ergibt sich der Umfang zu 2*Pi.
Dieses Bezeichnungssystem wird Radiant (Abk. rad) genannt, alternativ Bogenmaß.
Der Rechte Winkel im Einheitskreis ist hier Pi/2. Pi ist also relativ wichtig für das Bogenmaß, doch FreeBASIC bietet keine Möglichkeit, direkt an Pi heranzukommen. Pi läßt sich aus Tabellen oder mit anderen Programmen in jeder beliebigen Genauigkeit erhalten, doch ein übertrieben genaues Pi bringt bei der Berechnung nichts, da FreeBASIC die überflüssigen Stellen einfach nicht berücksichtigt. Was liegt also näher, als Pi mit FreeBASIC zu berechnen? Nichts.
Genauso, wie ich zu einem Winkel die Funktionswerte Sinus und Cosinus berechnen kann, läßt sich umgekehrt der Winkel aus dem Funktionswert errechnen. Bis auf zwei Ausnahmen sind aber alle Funktionswerte ziemlich lange Zahlen, betrachten wir also die Ausnahmen:
0 Nun der Winkel, der als Tangens 0 hat, ist 0(erstmal), das hilft hier nicht viel weiter..
1 (Die andere zentrale Ziffer der Computerwelt :D ), oh, da tut sich was, 0.7071..
Der ArcusTangens(das 'glauben' wir jetzt einfach mal) von 1 ist 0.7071..
FreeBASIC hat die Funktion ATN(), also ArcusTangens, bereits eingebaut, diese können wir nun benutzen:
0.7071 ist nun aber weit von Pi entfernt, genauer gesagt ist es Pi/4, also ist

..kuckean, so einfach ist das. Die Vereinbarung als Konstante(Const=) bewirkt, daß Pi im gesamten Programm nicht geändert werden kann. Das ist auch gut so, nach der ganzen Mühe, die wir hatten, um es zu erhalten.
Nun kennt das Bogenmaß aber nur Winkel, die sich als Bruchteil von Pi darstellen lassen, damit rechnet im täglichen Leben kein Mensch.
Im Allgemeinen rechnen wir mit einem Kreis, der 360°(Degree=Grad=>Deg als Abk. für diesen Modus) hat und die Zahlen werden dezimal dargestellt. Die alte Schreibweise mit Grad° Minuten' und Sekunden" wird hier (noch) nicht betrachtet.
Auch hier gibt es einen Winkel, der als Tangens 1 hat und der ArcusTangens von 1 ist 45°. Allerdings kann die ATN-Funktion diesen Wert nicht liefern, weil sie nur für das Bogenmaß gilt. Da nun aber ein Winkel in zwei Systemen bekannt ist, kann ich mir einen Umrechnungsfaktor berechnen, mit dem ich die Winkel von einem ins andere System umrechnen kann. Doch zuvor noch eine
NEBENBEMERKUNG:
Im Vermessungswesen ist es seit 1972 Vorschrift, eine andere Einteilung zu benutzen:
Der Vollkreis hat 400 gon. Damit ist der ArcusTangens von 1 gleich 50gon.
(Über die Vorteile dieses Systems schweige ich mich aber an dieser Stelle wider besseren Wissens einfach aus :D )
Weiter im Text.
In der Literatur wir meist 180/Pi als Umrechnungsfaktor angegeben. Sehen wir uns das genauer an, steht dort 4*45/(4*ATN(1)), und das ist nichts anderes, als 45/ATN(1). Wer kürzen kann, ist stark im Vorteil :D
Wir erkennen auch, das Programmieren eng mit Mathematik verbunden ist, doch das nur am Rande..
Den Umrechnungsfaktor von Deg nach Rad nennen wir Deg2Rad als Code

nun brauchen wir den umzurechnenden Winkel immer nur mit Deg2Rad zu multiplizieren und haben den Winkel im richtigen Modus.
Anders herum geht das auch, nur müssen wir dann eben teilen. Oder, weil es bequemer ist, definieren wir uns eine weitere Konstante Rad2Deg

Das geht auch mit nur einer Konstanten, allerdings kann es da schnell zu Verwechslungen kommen, da bei der Rückrechnung dann durch Deg2Rad geteilt werden muß(was gelegentlich vergessen wird/werden kann).
Natürlich läßt sich das auch per Function erledigen. Es gibt viele Wege einen Winkel ins Bogenmaß umzurechnen, aber eins ist Fakt:
Umgerechnet werden muß der Winkel, wenn er nicht im Bogenmaß ist.
Geschieht das nicht, ergeben sich oft nicht mehr nachzuvollziehende Ergebnisse, aber was noch viel schlimmer ist, sind die Fehler, die auftreten können, da ihre Ursache dann an der mglw. verkehrten Stelle gesucht wird.
Der einfachste Weg ist es, unmittelbar nach der Eingabe den Winkel gleich ins Bogenmaß umzurechnen und nur für die Ausgabe ggfs. ein anderes Format zu benutzen.

Winkelfunktionen
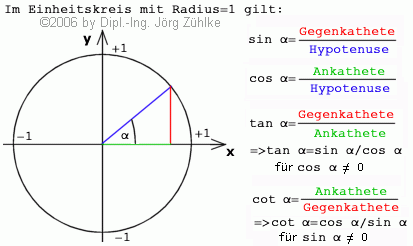
Winkelfunktionen sind nichts anderes, als Beziehungen, die sich aus einem Dreieck im Einheitskreis ableiten lassen.
Die Hauptwinkelfunktionen sind Sinus(FB-Funktion SIN() ) und CoSinus(FB-Funktion COS() ) alle anderen lassen sich hieraus berechnen. Aus diesem Grund hatte der Turbo-Pascal Compiler kein Tangens-Funktion, da sie sich eben aus Sinus und Cosinus ermitteln läßt:
Tangens=Sinus/Cosinus
Alles klar, dann schreiben wir uns eben mal eine Tangens-Funktion:

Wir brauchen uns dabei überhaupt keine Gedanken darüber zu machen, ob der Winkel größer als ein Kreis ist, denn die Periodizität der Winkelfunktionen garantiert immer richtige Werte.
Immer? Nicht ganz, denn das Verhältnis Sin(..)/Cos(..) ist auch eine Division und das heißt, sie ist nicht definiert, wenn der Divisor=0 ist, FreeBASIC würde 1.#Inf nehmen und weitermachen.
Alle weiteren Berechnungen mit diesem Wert wären dann aber, sagen wir mal, nicht unbedingt aussagekräftig, da 1.#inf.
Das ist, gelinde gesagt, unbrauchbar, denn eine Richtungsangabe mit 1.#inf ist zumindest 'nicht eindeutig' :D
Nun können wir davon ausgehen, daß im täglichen Gebrauch Cos(..) nicht 0 sein kann, was aber wenn doch?
Hier hilft uns wieder der Blick auf den Einheitskreis: Was ist denn, wenn der Cosinus eines Winkels 0 ist?Dann ist der Winkel 90°, Tangens wäre unendlich groß, also können wir ruhigen Gewissens die größte mit FreeBASIC darstellbare Zahl zurückgeben, das ist 1.0E+308, wobei das Vorzeichen dann vom Sinus abhängt..
Da diese Funktion bereits in FB implementiert ist, hier nochmal eine kompakte Version

Die geheimnisvolle Funktion Cotangens ist nichts weiter als der reziproke Wert vom Tangens, also doch kein Geheimnis.
Alle weiteren Funktionen müssen bei Bedarf aus der Literatur ermittelt und in ein Programm eingebaut werden.
Wie bereits gesagt, reicht es nicht aus, die Formeln 1:1 zu übernehmen, da ggfs. Sonderfälle zu berücksichtigen sind.

Gehe zu Seite  1  2  

Zusätzliche Informationen und Funktionen
Das Tutorial wurde am 14.06.2007 von ytwinky angelegt. Die aktuellste Version wurde am 28.12.2007 von ytwinky gespeichert.	Bearbeiten     Versionen